Scalar and Vector Quantities |Differences & Examples

by Richa Rastogi · Published March 6, 2023 · Updated October 17, 2024

In physics, a physical quantity is anything that can be measured, and it falls into one of two categories: scalar and vector quantities. Scalars are defined solely by their magnitude, while vectors require both magnitude and direction for a complete description.

The key difference between scalar and vector quantities lies in the presence of direction. While scalar quantities like distance or temperature can be fully described with a numerical value, vector quantities like velocity or force also need direction to convey their full meaning.

In this post, we’ll dive deeper into scalar and vector quantities, exploring examples and highlighting their differences. If you’re looking to learn more about physical quantities and measurements, check out our guide on Basics of Measurement for Kids.

SCALAR QUANTITY

Definition of a scalar quantity –

Scalar quantities are those physical quantities which are expressed only by their magnitude along with the unit required for the measurement.

For example, if we state that the mass of a bag is 5.0 kg, this information is complete by itself. It conveys both the amount (mass) and the unit of measurement (kilograms), without requiring any additional details such as direction. In this case, the mass is fully expressed as a scalar quantity because we don’t need to know where the bag is or in which direction it’s moving; the value and the unit are sufficient.

To completely define a scalar quantity, we need two essential components:

The numerical value of the measured quantity indicates “how much” of the quantity we are dealing with.
The unit in which the quantity is being measured, tells us the standard of measurement, such as kilograms, meters, or seconds.

Together, these provide the magnitude of the scalar quantity. Importantly, the magnitude is always positive, as it represents the size or amount of the quantity without the need for direction.

Examples of scalar quantities

Some of the examples of scalar quantities are – mass, time, length/distance, density, volume, temperature, speed, pressure, energy, power, charge, resistance, mechanical advantage, electric and magnetic potential, angle, etc.

We represent a scalar quantity symbolically by its English letter. For example, ‘m‘ denotes mass, ‘t’ time, ‘d’ distance, ‘s’ speed, etc. Scalar quantities can be added, subtracted, multiplied, and divided by simple mathematical methods.

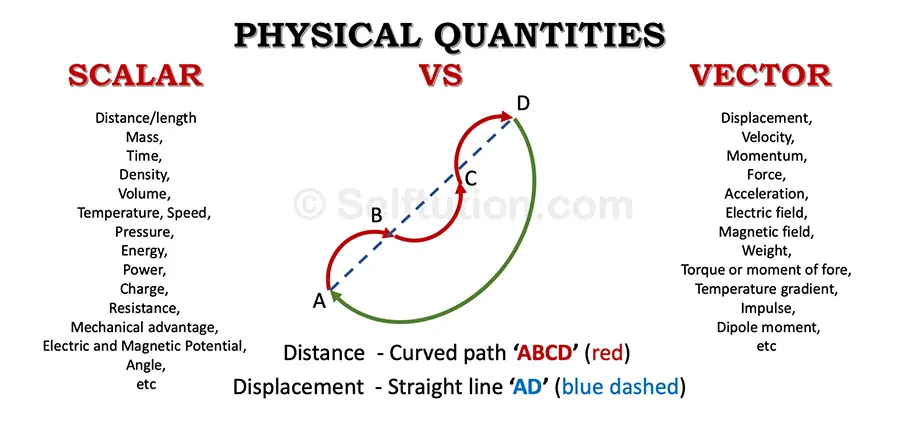
Difference between scalar and vector quantities with examples

VECTOR QUANTITY

Definition of a vector quantity –

Vector quantities are those physical quantities which require both magnitude and direction to represent them along with the unit required for the measurement.

For example, if we say “Displace a stone by 10 meters,” the first question that naturally arises is, “In which direction?” Without specifying the direction, the statement is incomplete. Displacement is not fully described by magnitude alone. However, if we say “Displace the stone by 10 meters towards the north,” the instruction becomes clear and meaningful.

To fully express a vector quantity, we require the following three components:

The numerical value of the measured quantity indicates the magnitude.
The unit in which the quantity is measured, such as meters, newtons, etc.
The direction of the quantity specifies where or in what direction the measurement is applied.

These three elements together—magnitude, unit, and direction—are essential to completely describe a vector quantity. Without any one of them, the description remains incomplete.

The numerical value of a vector quantity along with its unit gives us the magnitude of the quantity. The negative sign with a vector quantity implies a reverse or opposite direction. Thus, vector quantities can be positive as well as negative.

Examples of vector quantities

Some of the examples of vector quantities are – displacement, velocity, force, acceleration, electric field, magnetic field, weight, torque, temperature gradient, etc.

A vector quantity is generally written symbolically by its English letter bearing an arrow on it. Sometimes vector quantity is also represented by a bold English letter. For example, ‘d‘ denotes displacement, ‘v‘ velocity, ‘a‘ acceleration, ‘F‘ force, etc. Kindly note, that ‘F‘ and ‘- F‘ are two equal forces acting in opposite directions. We cannot perform simple mathematical operations on vector quantities, unlike scalar quantities. Vector quantities follow different algebra for their addition, subtraction, and multiplication.

DIFFERENCE BETWEEN SCALAR AND VECTOR QUANTITIES

Scalar quantities are those physical quantities that are expressed only by their magnitude whereas vector quantities require both magnitude and direction to completely express them.
The scalar quantities are always positive whereas vector quantities can be positive as well as negative.
A simple mathematical operation can be performed on scalar quantities whereas vector quantities follow complex algebra for their addition, subtraction, and multiplication.

Difference between scalar and vector quantities in tabular form: